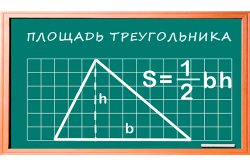Треугольником называется фигура на плоскости, состоящая из трех сторон и трех вершин и ограничивающаяся отрезками трех прямых, которые попарно пересекаются. Каждая вершина обычно обозначается латинскими прописными буквами (пусть, например, А, В и С). Каждая сторона - парой букв, отвечающих углам, между которыми эта сторона расположена (в примере - АВ, BC и АС).

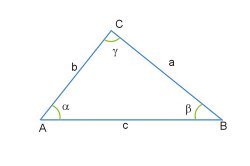Перед тем как найти площадь треугольника может понадобиться определить некоторые его характеристики: величины сторон, которые обозначаются маленькими латинскими строчными буквами (в примере - a, b и c), и величины внутренних углов, которые обозначаются строчными греческими буквами (в примере - α, β и γ).

Далеко не всегда в качестве начальных данных дается достаточно параметров, чтобы определить площадь фигуры. Решить треугольник (вычислить его размеры и площадь) можно всего в трех случаях:
- когда заданы две стороны и значение лежащего между ними угла. Этих исходных данных вполне достаточно, чтобы напрямую воспользоваться одной из формул для определения площади без дополнительных вычислений.
- когда известна одна сторона и величины двух прилежащих к ней углов. Третий угол определяется в такой ситуации однозначно. А неизвестные стороны могут быть вычислены по теореме синусов. После уточнения значения хотя бы одной дополнительной стороны данных для расчета площади треугольника вполне достаточно.
- когда у треугольника заданы величины всех трех сторон. В этом случае для определения площади можно применить формулу Герона, и тогда в вычислении величин углов (по теореме косинусов) не будет необходимости.

Существует много формул, которые позволяют определить площадь любого треугольника. Выбор подходящей зависит только от того, какие величины у треугольника или уже известны, или легко и быстро могут быть найдены.

Наиболее широко известна такая формула: площадь треугольника равна произведению стороны на половину высоты, проведенную к этой стороне. Например, для стороны ВС противолежащей является вершина А. Из это вершины опускаем перпендикуляр на сторону ВС (либо на ее продолжение). Такая высота, как правило, обозначается ha. И тогда площадь определяется выражением: S = a * ha / 2.

Еще одна распространенная формула: площадь треугольника равняется произведению двух сторон на половину синуса угла, расположенного между ними. Она напрямую связана с предыдущим выражением для определения площади, поскольку высота как раз и вычисляется через одну из сторон и прилежащий к ней угол. Например, между сторонами АС (длиной b) и ВС (длиной a) лежит угол С (величиной γ). Итак, S = b * а * sin(γ) / 2.

Формула Герона (как и первая формула) для применения тоже требует предварительного определения дополнительного параметра. Он называется полупериметром (р) и вычисляется как полусумма длин всех сторон треугольника: p = (с + b + а) / 2. Окончательно формула Герона имеет такой вид: S = (p*(p-a)*(p-b)*(p-c))^ ½, где обозначение ^ означает функцию возведения в степень. Стоит отметить, что возведение в степень ½ равносильно извлечению корня из получившегося значения.

Отдельное внимание всегда уделяется особым типам треугольников. Они классифицируются либо по углам, либо по сторонам. В зависимости от величин углов треугольники делятся на остроугольные, тупоугольные и прямоугольные. Последние характеризуются обязательным наличием у треугольника угла величиной 90º. Стороны, которые образуют этот прямой угол называют катетами (а и b), а противолежащую сторону называют гипотенузой (c). Наличие однозначно известного угла напрямую влияет на то, как найти площадь прямоугольного треугольника. Широко распространена такая формула: площадь треугольника с прямым углом равняется произведению катетов, деленному пополам. А точнее: S=a*b/2.

В зависимости от величин сторон выделяют такие типы треугольников: равнобедренные и равносторонние. Последние характеризуются равенством всех трех сторон (с=b=а), а также равенством всех трех углов (α = β = γ = 60º). Для треугольников особого вида, безусловно, можно использовать стандартные формулы, и они дадут правильный результат. Но в некоторых случаях имеет смысл применять давно известные выражения, которые существенно ускоряют процесс вычислений. Так как найти площадь равностороннего треугольника, например, можно опираясь только на значение величины стороны. Она пропорциональна квадрату стороны с коэффициентом (3/16)^ ½. То есть S= (3/16)^ ½ * a^2.